Числовые диковинки Перельмана или арифметические фокусы

Яков Исидорович Перельман (1882-1942), российский и советский математик, физик и мировед, журналист и педагог, популяризатор точных наук, основоположник жанра занимательной науки. Кстати, распространено заблуждение, что Яков Перельман является отцом известного математика Григория Перельмана, это не так — первый умер более чем за 20 лет до рождения второго.

 

 

Яков Исидорович Перельман. Источник фото: aftershock.news.

Честно говоря, зачиталась и очень советую любителям математики её прочитать. Одна из глав этой книги называется «Галерея числовых диковинок», в ней собраны числа, обладающие исключительными особенностями. Очень интересно автор говорит, что эти числа можно было бы собрать в музей числовых редкостей, настоящую «арифметическую кунсткамеру». Вот некоторые:

 

Число 365

• Оно замечательно прежде всего тем, что определяет число дней в году;
• 365 = 10×10 + 11×11+12×12, т. е. число 365 равно сумме квадратов трёх последовательных чисел, начиная с 10:

 

 

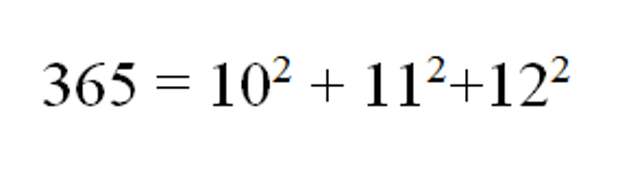
Но это ещё не всё,

 

 

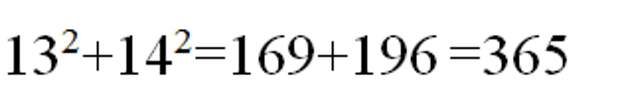
• На этом свойстве числа 365 основана задача С.А. Рачинского, изображённая на известной картине «Трудная задача» Богданова-Бельского:

 

 

 

 

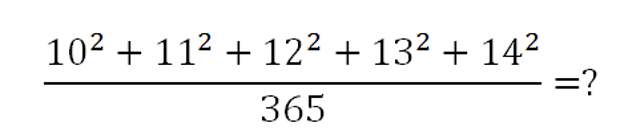
Николай Петрович Богданов-Бельский картина "Трудная задача. В народной школе С.А. Рачинского" 1895 год.

Число 999

Наибольшее из всех трёхзначных чисел.

Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа: получается шестизначное число, первые три цифры его есть умножаемое число, уменьшенное на единицу, а остальные три цифры (кроме последней) — «дополнения» первых до 9. Например:

358 × 999 = 357 642

826 ×999 = 825 174

453 ×999 = 452 547

751 ×999 = 750 249 (надеюсь, вы догадались. как получить последнюю цифру у числа?).

Происхождение этой особенности числа 999 легко понять, стоит лишь взглянуть на следующую строчку:

 

 

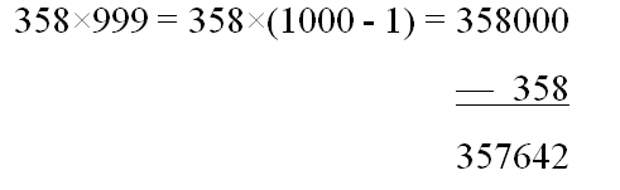
Перельман, кстати, предлагает свойства этих чисел использовать в качестве «фокусов» перед непосвящёнными. И на примере следующей диковинки я это покажу.

Число 1001 — число Шехерезады

Чем же оно замечательно? С виду вполне обыкновенное, и даже не является простым числом. Оно делится без остатка и на 7, и на 11, и на 13 — на три последовательных простых числа, причём 1001 = 7 ×11×13. Но диковинка не в этом.

Замечательно оно тем, что при умножении на него трёхзначного числа получается результат, состоящий из самого умножаемого числа, записанного дважды:

243×1001 = 243 243

528×1001 = 528 528

Это понятно, так как 243×1001 = 243×1000 + 243.

Автор предлагает это свойство использовать как ФОКУС, в компании друзей:

1. Предложите кому-нибудь записать на бумажке (втайне от вас) любое трёхзначное число;
2. Затем пусть он (или его сосед) припишет к нему ещё раз то же самое число. Получится шестизначное число из трёх повторяющихся цифр.
3. Предложите разделить это число на 7 (подсказывая, что число разделится без остатка);
4. Результат передаётся новому соседу, которому предлагается разделить полученное число на 11;
5. Полученное число передаёте другому, которого просите разделить это число на 13;
6. Результат третьего деления вы, не глядя на полученное число, вручаете первому, загадавшему число со словами:

— Вот число, которое вы задумали!

А вы поняли, в чём разгадка фокуса???